TESSELLATIONS
In 1900, David Hilbert (1862 - 1943) proposed a total of 23 problems about
different areas of mathematics. 18th of these problems was about building spaces with congruent polyhedra. Later, this topic
has been widely studied and is still being studied.
The
regular tiling of polygons or polyhedra (or polytopes in general) is called a tessellation. Tessellations in two
dimensions are abundantly studied, but tessellations in higher dimensions still
need to be extensively explored. A recent thesis published about space-filling
polyhedra belongs to Kara Joy Duckett. [Duckett, K. J., Close-Packing Polyhedra: Three Dimensional Tessellations, Department of Mathematics and Computer Science,
Meredith College, 2003 – the thesis is available online at page http://www.angelfire.com/nc3/karaduckettthesis/] Some three dimensional tessellation examples of Ducket
are given below:


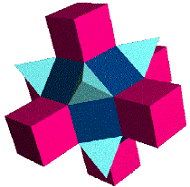



Another mathematician working on
space-filling polyhedra is Guy Inchbald. Three of his original
space-filling polyhedra (the
bisymmetric hendecahedra, The sphenoid hendecahedra, The rhombic
dodecahemioctahedron) are illustrated below:
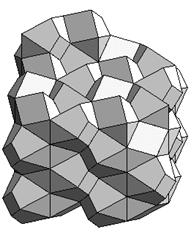
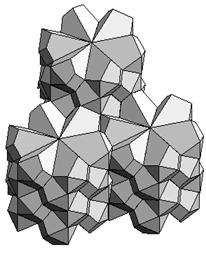
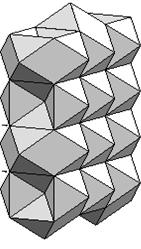
Three of Inchbald’s
tessellations [http://www.queenhill.demon.co.uk/polyhedra/five_sf/five.htm]
