POLYHEDRAL LINKAGES

In the need for combining the fascinating geometry of polyhedra and motion, inventors and engineers found a new area of study for themselves: polyhedral linkages. Not much has been done about the subject yet, however, it seems that the subject will be of concern for many years.

Engineers had a lot of beautiful examples before they started working on the subject: An American investigator’s, Chuck Hoberman’s, amazing toys were ready to work on.

Two of the Hoberman toys

The Hobermans also have architectural products. The huge domes they make are well accepted all aroun the world (See [http://hoberman.com] for more examples and animations)

The iris dome (left), the retrect dome (second) and the fabric dome (last two) of Hoberman Associates

The huge gate used in 2002 Olympic Games

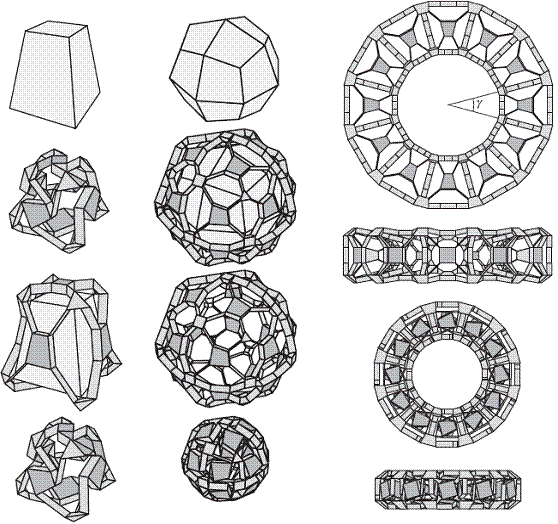
Having these fantastic examples at hand, mechanical engineers developed some methods to mobilize the polyhedra. One of the engineers working on the subject is Karl Wohlhart. Wohlhart makes use of rotational type joints to expand and contract polyhedra. In 2001 he presented his method for uniform polyhedra (See [Wohlhart, K., Regular Polyhedral Linkages, Proceeding of the 2nd Workshop on Computational Kinematics, pp. 239-248, Seoul, 2001]). Here are some of his designs:

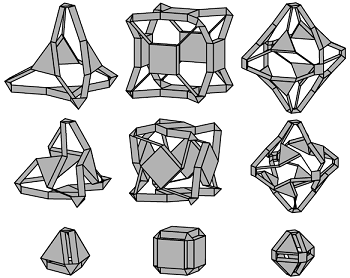
The five Platonic solids, a prism, the truncated icosahedron

and a rhombic polyhedron mobilized by Wohlhart

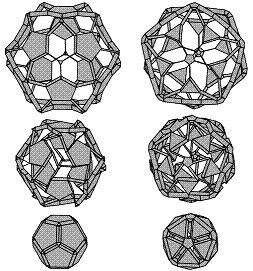
Later in 2004, Wohlhart applied his method to non-uniform polyhedra as well. But there is no wide range of examples for nonuniform polyhedra (See [Wohlhart, K., Irregular Polyhedral Linkages, Proceedings of the 11th World Congress in Mechanism and Machine Science, pp. 1083-1087, Tianjin, 2001])

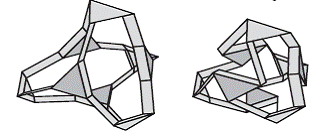
A non-uniform tetrahedral and a nonuniform hexahedral linkage

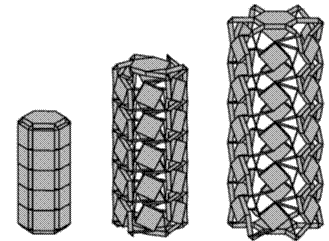
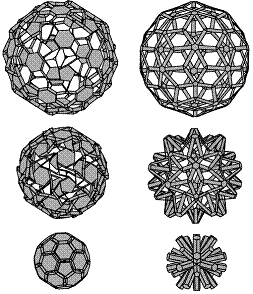
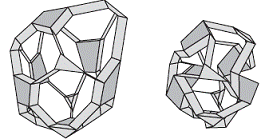
He also gives examples for frustum pyramids and Catalan solids (duals of Archimedean solids) together with a beautiful toroidal linkage complex:

A frustum pyramid and a Catalan solid and a toroidal linkage complex

Another method for design of polyhedral Linkages was proposed by Agrawal et al. in 2002 (See [Agrawal, S. K., Kumar, S., Yim, M., Polyhedral Single Degree-of-freedom Expanding Structures: Design and Prototypes, Journal of Mechanical Design, Volume 124, Issue 3, pp. 473-478, 2002] They placed the joints at the edges instead of the vertices, and they used prismatic [sliding] joints instead of revolute (rotational) joints. They also considered combining these linkages together to model three dimensional objects.

These are not the only designs of these inventors and researchers and some other related designs belong to Goldberg, Fuller and Verheyen, Tarnai et. al., Gosselin et. al. and Kiper et. al.