GREEKS

There are many thinkers that worked on polyhedra among the ancient Greeks. However, focus on Plato’s work will be kept in this document.

Early civilizations worked out mathematics as problems and their solutions. According to B. L. van der Waerden there are so many similarities between the studies of Egyptians, Babylonians, Chinese and also Indians that he believes that these different civilizations’ work originate from a common source. He proposes that all these cultures are affected by studies carried on in the Neolithic Age, say between 3000 and 2500 BC. [B. L. van der Waerden, Geometry and Algebra in Ancient Civilizations, Springer – Verlag, 1983, pxi] However, ancient Greeks’ approach is totally different: proofs are indispensable parts of analyses.

Cromwell, in his Polyhedra, mentions the probability that Greek mathematicians, who liked traveling a lot, needed proofs to decide whether Babylonians’ methods or Egyptian’s methods are the true ones.

Plato (427- 347 BC)

Plato, when the concern is polyhedra, is most well known as the comments on the five regular polyhedra, which are named after him. Although the regular polyhedra are called the Platonic solids, Plato was not the first to recognize them. Pythagoreans already knew three of them for their regularity: the cube, the tetrahedron (they would call it a pyramid) and the dodecahedron. Theaetetus, a friend of Plato, is known to first discover the regularity the icosahedron and the octahedron. It must be emphasized that these solids were already known to people, but Pythagoreans and Theaetetus were the ones discovering their regularity. Plato’s contribution to the subject was not discovering the regular polyhedra, but associating them to the elements constructing the world.

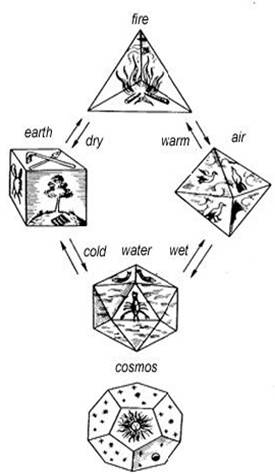
Johannes Kepler’s interpretation of the Platonic solids – basic elements association

To earth, then, let us assign the cubic form, for earth is the most immovable of the four and the most plastic of all bodies, and that which has the most stable bases must of necessity be of such a nature. Now, of the triangles which we assumed at first, that which has two equal sides is by nature more firmly based than that which has unequal sides, and of the compound figures which are formed out of either, the plane equilateral quadrangle has necessarily a more stable basis than the equilateral triangle, both in the whole and in the parts. Wherefore, in assigning this figure to earth, we adhere to probability, and to water we assign that one of the remaining forms which is the least movable, and the most movable of them to fire, and to air that which is intermediate. Also we assign the smallest body to fire, and the greatest to water, and the intermediate in size to air, and, again, the acutest body to fire, and the next in acuteness to air, and the third to water. Of all these elements, that which has the fewest bases must necessarily be the most movable, for it must be the acutest and most penetrating in every way, and also the lightest as being composed of the smallest number of similar particles, and the second body has similar properties in a second degree, and the third body, in the third degree. Let it be agreed, then, both according to strict reason and according to probability, that the pyramid is the solid which is the original element and seed of fire, and let us assign the element which was next in the order of generation to air, and the third to water. We must imagine all these to be so small that no single particle of any of the four kinds is seen by us on account of their smallness, but when many of them are collected together, their aggregates are seen. And the ratios of their numbers, motions, and other properties, everywhere God, as far as necessity allowed or gave consent, has exactly perfected and harmonized in due proportion.

[Plato, Timaeus, p1181]

Ancient Greeks believed that the physical world was made up of four basic elements and their combinations: fire, air, water and earth. Fascinated by the various beautiful aspects of the regular polyhedra, Plato imagined a world consisting of them. With his own reasonings he assigned each of the regular polyhedra to a basic element. But there still remains one polyhedron out when four of them are assigned to the four basic elements. Plato associated the remaining polyhedron, the dodecahedron, to the universe, and named a fifth element: ether (For more information please refer to http://www.mlahanas.de/Greeks/PlatoSolid.htm).

This association plays great role in Plato’s Timaeus, the article he has written for his friend Theaetetus, who died after having serious injuries in a battle. His theses were so harmonic and smooth that this vision of the cosmos affected many philosophers, mathematicians and artists. The Lord’s perfect world had to be constructed with perfect geometrical shapes:

As God brought into being the celestial virtue, the fifth essence, and through it created the four solids . . . earth, air, water, and fire ... so our sacred proportion gave shape to heaven itself, in assigning to it the dodecahedron . . . the solid of twelve pentagons, which cannot be constructed without our sacred proportion. As the aged Plato described in his Timaeus.

[Pacioli, L., De Divina Proportione, 1509]

The «sacred proportion» Pacioli refers to is the golden ratio (The edges of a dodecahedron can be obtained by placing three mutually orthogonal rectangles having golden ratio as the ratio of the side lengths in a symmetric manner).

The Sacrament of the Last Supper by Dali

Because of his work about the five regular polyhedra, Plato is known as the first scientist proposing an atomic model for the matter.

At this point, we shall focus on a conjugation property of polyhedra: duality. Roughly speaking, the dual of a polyhedron is obtained by replacing the faces of a polyhedron with vertices and vice versa. Theoretically all the polyhedra have duals, but not all are finite polyhedra. The duals can be obtained by connecting geometric centers of the faces, resulting a new polyhedron inside. This operation is illustrated below for the tetrahedron, the cube and the icosahedron:

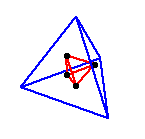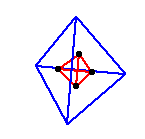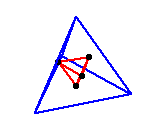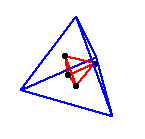
Duals of Platonic solids

It can be showed that dual of the dual of a polyhedron is itself. So duality is a conjugation. From the above figure, one can see that duals of Platonic solids are again platonic solids. Tetrahedron is self-dual, while cube-octahedron and icosahedron-dodecahedron couples are duals of each other. A polyhedron combined with its dual constitutes a compound polyhedron. The duals, and compounds for the platonic solids are given below:

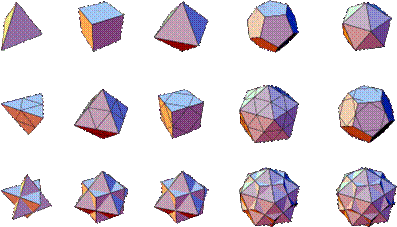
Duals and compounds for the Platonic solids

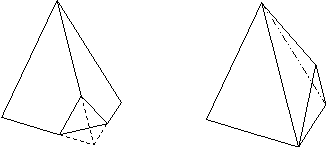
Truncation and expansion

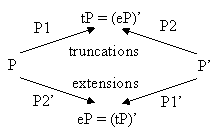
Two duals also can be obtained from each other by means of truncations and expansions (snubbing/extension/augmentation). Proper truncations (cuttings of regular pyramids on each vertex) or extensions (assemblings of regular pyramids on each face) of dual polyhedra give the same polyhedron. [http://www.ac-noumea.nc/maths/amc/polyhedr/sequences_.htm] For the dual polyhedra P and P’, this fact can be shown in the following diagram (P1-P1’, P2-P2’ and tP-eP are duals of each other; P1-P1’, P2-P2’ are forms in between P, P’ and tP, eP):

For the Platonic solids, the following series can be considered:

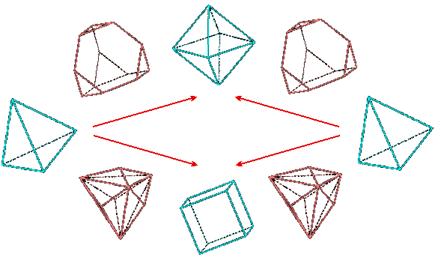
Tetrahedron-to-tetrahedron (tP = octahedron, eP = cube)

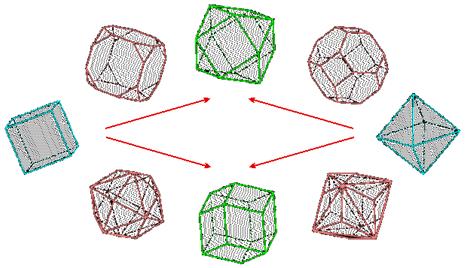
Cube-to-octahedron (tP = cuboctahedron, eP = rhombic dodecahedron)

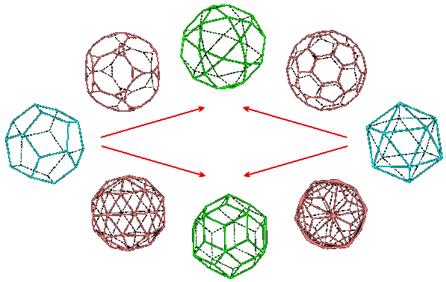
Dodecahedron to icosahedron (tP = icosidodecahedron, eP = rhombictriacontahedron)

The seven non-Platonic truncated figures shown in these three figure are Archimedean solids and the corresponding duals are Catalan solids (See the next section for information in detail).

Plato did not give a proof that there are only five regular polyhedra. Actually, he did not even formally specify the properties a regular polyhedron must satisfy. The first of the proofs was given by an Alexandrian mathematician: Euclid.