RENE DESCARTES
René Descartes (1596-1650)
Just like the other revolutions
Descartes made in many scientific areas, the new approach he imposed in
polyhedral geometry is a radical attempt. Descartes is the first scientist who explored
polyhedra in general and deduced the properties of special polyhedra as special
cases of the general results he obtained. His work on polyhedra gave birth or
influenced many branches of mathematics.
Especially one theorem of Descartes
(presented in his Progymnasmata de Solidorum Elementis (1630)) about polyhedra is charming: the sum
of deficiencies of the solid angles in a polyhedron is eight right angles (The
proof follows immediately from the Spherical
Excess formula). This theorem is “A very beautiful and general theorem
which ought to be placed at the head of the theory of polyhedra” according to
E. Prouhet.
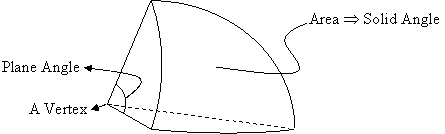
For polyhedra, the solid angle is a quantity assigned to a
vertex. It is the area of the unit sphere portion corresponding to the vertex.
Its unit is steradians.
The angle by which the sum of the plane angles around a solid angle is less
than 2p is called its deficiency.
One of the
corollaries of Descartes’ theorem is that there can be only five regular
polyhedra. Consider a polyhedron with V vertices,
with each surrounded by S faces of
each having n equal length sides.
Then the sum of interior angles of a face is (n - 2)p and so, every
plane angle measures (n - 2)p/n. S
plane angles meet at V vertices, so
the sum of plane angles is SV(n - 2)p/n. By the theorem,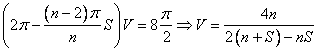 
. The denominator can be factorized as 
, which implies that 
must be less than 4.
The possible integer pairs for (n, S) are then (3, 3), (3, 4), (3, 5), (4,
3) and (5, 3), which describes the tetrahedron, the octahedron, the icosahedron, the cube and the dodecahedron, respectively
and uniquely. As opposed to
