ALEXANDRIANS

Alexandria was the center of scientific investigations of its time; and the most popular researchers of Alexandria are Euclid and Archimedes.

Euclid (325 – 265 BC)

Euclid proves that there are no regular polyhedra other than the five Platonic solids as a remark at the end of 18^th proposition of 13^th book of his Elements (the English translation of Elements can be found at http://aleph0.clarku.edu/~djoyce/java/elements/toc.html). His claim also defines what a regular solid is: no other figure, besides the said five figures, can be constructed which is contained by equilateral and equiangular figures equal to one another. Euclid’s definition of regular polyhedra is, however, incomplete. It would be complete if he also included the condition that each vertex should join equal number of faces. There exist five more polyhedra satisfying Euclid’s original definition: the deltahedra. These are equilateral triangle faced polyhedra. There are totally eight convex deltahedra; three of which are regular polyhedra (tetrahedron, octahedron, icosahedron, triangular dipyramid, pentagonal dipyramid, tri-augmented triangular prism, gyro-elongated square dipyramid, Siamese dodecahedron).

Euclid’s proof is very straightforward, simple and short: he just analyses the possible number of possible regular polygons that can meet at a vertex and comes up with the only five possibilities. In addition to this proof, Euler has more than twenty propositions relating polyhedra. He, like Liu Hui, sometimes uses dissections:

Euler constructs the dodecahedron by placing roofs on faces of a cube

Archimedes (287 – 212 BC)

Archimedes is a Greek mathematician and engineer born and died in Sicily, but he has probably studied in Alexandria for a long period. He is, to many mathematicians, one of the three greatest mathematicians of all time (the other two are Isaac Newton and Carl Friedrich Gauss). [http://www.mcs.drexel.edu/~crorres/Archimedes/Solids/Pappus.html] The thirteen semi-regular polyhedra are named after him. A key characteristic of the Archimedean solids is that each face is a regular polygon, and around every vertex, the same polygons appear in the same sequence.

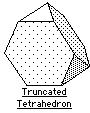
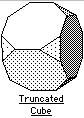
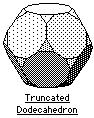
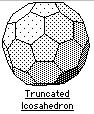
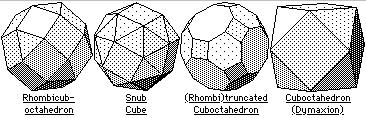
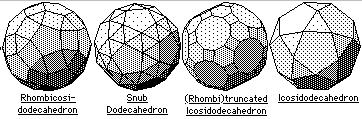
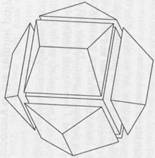
The thirteen Archimedean solids

The Archimedean solids, somewhat, can be derived using the Platonic solids. Nine of them be obtained by truncation of a Platonic solid, and two further can be obtained by a second truncation. The remaining two solids, the snub cube and snub dodecahedron, are obtained by moving the faces of a cube and dodecahedron outward while giving each face a twist (For details about truncations and snubbing, please see Duckett, K. J., Close-Packing Polyhedra: Three-Dimensional Tessellations, 2003 – presented on webpage http://www.angelfire.com/nc3/karaduckettthesis/). Two of the truncation series are as follows:

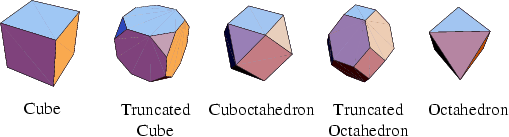
Two truncation series: cube to octahedron, icosahedron to dodecahedron.

The duals of the Archimedean solids are called the Catalan solids (named after the Belgian mathematician Eugéne Catalan - 1865). The Archimedean solids and the duals of them are presented below:

cuboctahedron	rhombic dodecahedron
great rhombicosidodecahedron	disdyakis triacontahedron
great rhombicuboctahedron	disdyakis dodecahedron
icosidodecahedron	rhombic triacontahedron
small rhombicosidodecahedron	deltoidal hexecontahedron
small rhombicuboctahedron	deltoidal icositetrahedron
snub cube	pentagonal icositetrahedron
snub dodecahedron	pentagonal hexecontahedron
truncated cube	Small triakis octahedron
truncated dodecahedron	triakis icosahedron
truncated icosahedron	pentakis dodecahedron
truncated octahedron	tetrakis hexahedron
truncated tetrahedron	triakis tetrahedron

Some mathematicians had argued that there is one more semi-regular polyhedron: the elongated square gyrobicupola:

Today, it is known that this solid does not belong to the set that the thirteen Archimedean solids constitute because of lacking the symmetry level the other solids have.